Complement of a Set
Complement of a set
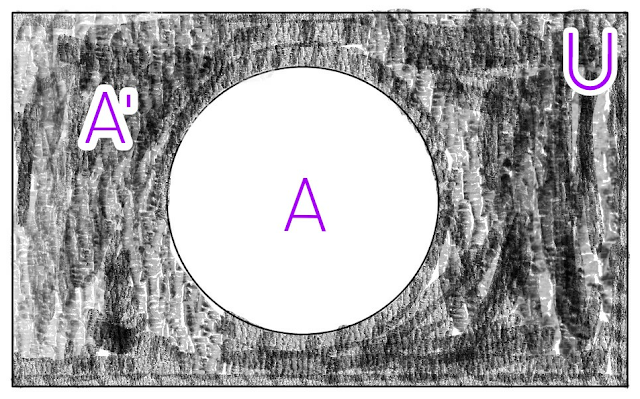 |
| Fig (10) |
 |
| Fig (10) |
Energy interaction (Transition) An energy interaction or transition is said to occur or to exist between two systems when one system influences a sustains the state of the other system. Thermodynamics mainly studies the interactions between heat and work and associated property change of the system In otherwords Energy…
Ideal gases The term gas is applied to a particular phase of a pure substance which will fills the system boundary, and no change of phase takes place or is contemplated. They always exist in gaseous form. For this reason, they have been called permanent gases. Perfect…
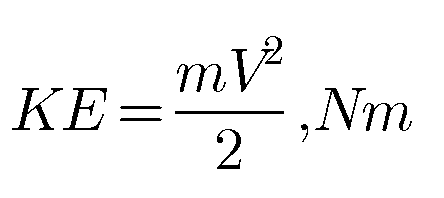
Energy in a state Stored energy is the energy possessed by a system. Stored energy in the system is called energy in a state. It is associated with a state. It change depends only on the end states of the process and not on the path of…
First Law for a Closed System Undergoing a Quasi-static process In many occasions it is necessary to consider a system undergoing a process rather than a cycle. The equation, ∮ dQ − ∮ dW = 0 is applicable during the system undergoing a cycle, and algebraic sum of all energies transfer across the system boundary…
Reversible and Irreversible processes A process which can be reversible i.e., operated in opposite direction from any state during the process such that the system returns to its initial state and their may be no effect on the surroundings. Thus at the end of the process both the system and…
Conservation of Energy In the early part of 19th century the scientist developed the concept of energy and hypothesis that it can be neither created nor destroyed ; this come to be known as the law of the conservation of energy. The first law of thermodynamics is merely one statement of this…