Similar Posts
Universal Set
Universal set In any discussion in set theory, there always happens to be a set that contains all sets under consideration i.e. it is a super set of each of the given sets. Such a set is called the universal set and is denoted by U. Thus a set that contains all sets in a…
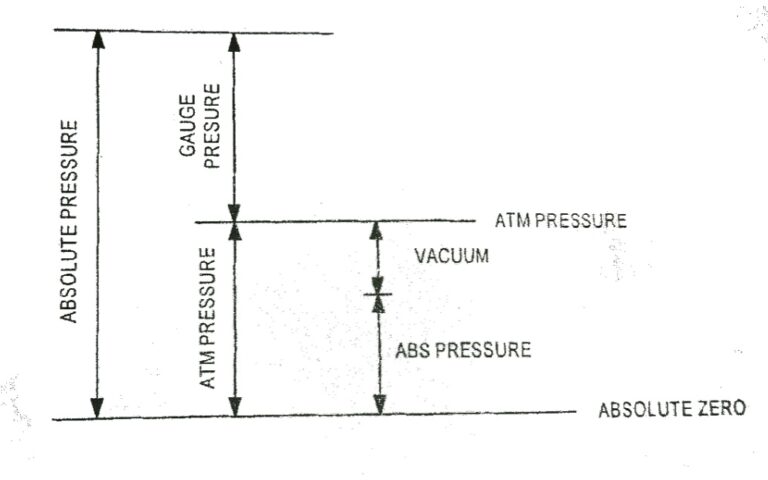
Pressure | Absolute Pressure | Atmospheric Pressure | Pressure Guage Barometer, Bourdon, U-tube manometer
Pressure The molecules of a gas are in random motion. The rapidly moving molecules continually impact on the surface of the container and its effect is to produce a force over the surface. The force normal to unit area of surface is called pressure acting on the surface. The normal force exerted by the atmosphere…
Introduction about Thermodynamics and Application of Thermodynamics
Introduction about thermodynamics Energy is the capacity to do work energy cannot be created or destroyed but only can be changed into other forms (principle of conservation of energy). Thermodynamics mainly deals with interaction between heat and work (mechanical energy) and change in the property is associated with these interactions. The interaction between heat and…
Symmetry Difference of Sets
Symmetry difference of sets Let A and B be two sets. The symmetry difference of sets A and B is the set (A-B) ∪ (B-A) and it is denoted by A ∆ B. Then A∆B=(A-B) ∪ (B-A) = {x : x ∉ A ∩ B}. In Fig 9 shaded region represents A∆B Fig (9) Example…
Difference of Sets
Difference of sets Let A and B be two sets. The difference of A and B written as A – B, is the set of all those elements of A which do not belong to set B Thus A – B={ x : x ∈ A and x ∉ B} or A – B={ x…
SI (System of International) System of Units
SI (System of international) system of units The SI system consists of seven basic units and two supplementary units. These are represented in table 1 . The unit for other quantities are derived from the basic units which are given in table 2. It is convenient to use prefix to avoid the use of very…
