Similar Posts
Power Set
Power set Let A be a set. Then the collection or family of all subsets of A is called the power set of A and is denoted by P(A). That is. P(A) = { S : S ⊂ A }. Since the empty set and the set A itself are subsets of A and are…
What are Reversible and Irreversible Processes in Thermodynamics | Causes of Irreversible
Reversible and Irreversible processes A process which can be reversible i.e., operated in opposite direction from any state during the process such that the system returns to its initial state and their may be no effect on the surroundings. Thus at the end of the process both the system and…
Function as a Set of Ordered Pairs
Function as a set of ordered pairs Let A and B be two non-empty sets. A relation f from A to B i.e a subset of A × B is called a function (or a mapping or a map) from A to B, if i) for each a ∈ A there exists b ∈ B…
What is Relation in Mathematics
Relation Let A and B be two sets. Then a relation from set A to B is a subset of A × B. Thus, R is a relation from A to B⇔R ⊆ A × B. If R is a relation from a non-void set A to non-void set B and my if (a, b)…
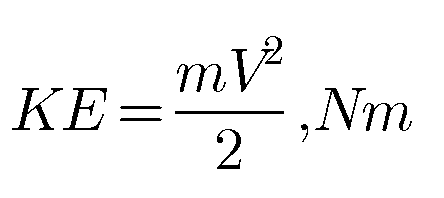
Energy in a State | Point and Path Functions in Thermodynamics
Energy in a state Stored energy is the energy possessed by a system. Stored energy in the system is called energy in a state. It is associated with a state. It change depends only on the end states of the process and not on the path of…
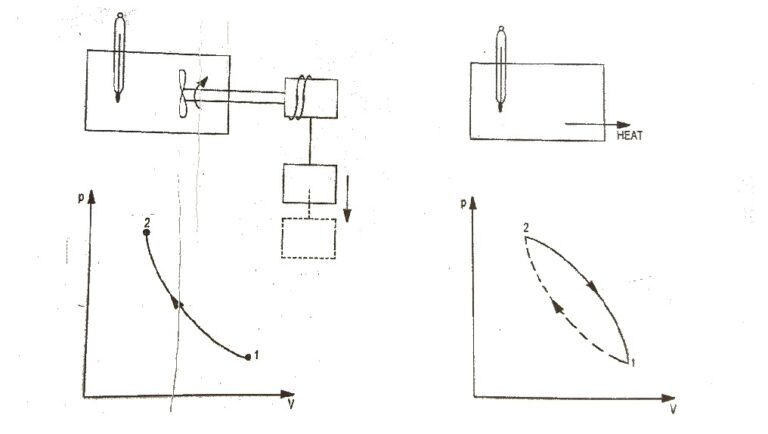
First Law of a Closed System Undergoing a Cycle
First Law of a Closed System Undergoing a Cycle : The first law of thermodynamics states that during any cycle a system undergoes the cyclic integral of heat is equal to the cyclic integral of the work. Fig.1 First Law of Thermodynamics To illustrates this, consider the gas as a system in…

Nice
Nice
Nice