Ordered Pairs and Equality of an Ordered Pairs
Ordered pairs
An ordered pairs consists of two objects or elements in a given fixed order.
An ordered pairs consists of two objects or elements in a given fixed order.
Power set Let A be a set. Then the collection or family of all subsets of A is called the power set of A and is denoted by P(A). That is. P(A) = { S : S ⊂ A }. Since the empty set and the set A itself are subsets of A and are…
Thermodynamic system Thermodynamic system is defined as quantity of matter or a region in a space chosen for study. Everything external to the system is called surroundings. The system is separated from the surroundings by the boundary that may be real or imaginary The boundary does not intervene between the system and surroundings. It only…
Reversible and Irreversible processes A process which can be reversible i.e., operated in opposite direction from any state during the process such that the system returns to its initial state and their may be no effect on the surroundings. Thus at the end of the process both the system and…
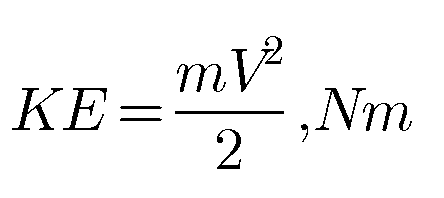
Energy in a state Stored energy is the energy possessed by a system. Stored energy in the system is called energy in a state. It is associated with a state. It change depends only on the end states of the process and not on the path of…
Difference of sets Let A and B be two sets. The difference of A and B written as A – B, is the set of all those elements of A which do not belong to set B Thus A – B={ x : x ∈ A and x ∉ B} or A – B={ x…
Thermodynamic equilibrium Thermodynamic state is a condition of a system and is specified by its thermodynamic properties. Thermodynamic Equilibrium of a system is a state such that if the system is isolated from its surroundings no change in thermodynamic properties would occur. A system will be in a state of thermodynamic equilibrium if the conditions…