Properties of Ideal gases ∣ Charactaristic of gas equation ∣ Specific Heat
Ideal gases
Boyle and Charles investigated the behaviour of gases and formulated the laws.
Function as a set of ordered pairs Let A and B be two non-empty sets. A relation f from A to B i.e a subset of A × B is called a function (or a mapping or a map) from A to B, if i) for each a ∈ A there exists b ∈ B…
Power set Let A be a set. Then the collection or family of all subsets of A is called the power set of A and is denoted by P(A). That is. P(A) = { S : S ⊂ A }. Since the empty set and the set A itself are subsets of A and are…
Types of relation Void relation:- Let A be a set. Then, Φ ⊆ A x A and so it is a relation on A. This relation is called the void or empty relation on set A. In other words, a relation R on a set A is called void or empty relation, if no element…
Macroscopic and Microscopic Approaches The behaviour of matter can be studied by two approaches 1. Macroscopic approach, 2. Microscopic approach 1. Macroscopic approach – In the macroscopic approach a certain quantity of matter is considered for study without knowing the behaviour of individual…
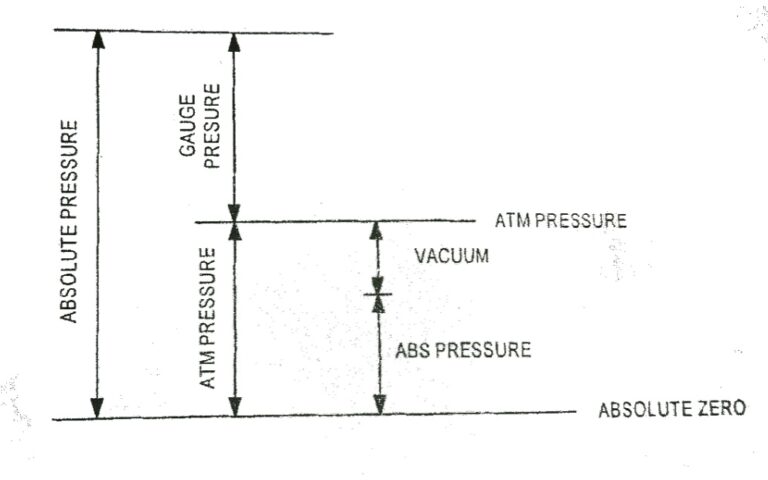
Pressure The molecules of a gas are in random motion. The rapidly moving molecules continually impact on the surface of the container and its effect is to produce a force over the surface. The force normal to unit area of surface is called pressure acting on the surface. The normal force exerted by the atmosphere…
State, path and process State A state is condition of system and is specified by its properties. At a given state all the properties of a system have definite values Path Change of state of a system is the consequence of any operation in which properties will change. The series of states through which system…
Hello
How can i help you