The total number of subsets of a Finite Set containing n elements is 2ⁿ
We will discuss later in permutation and combination chapter in brief.
Universal set In any discussion in set theory, there always happens to be a set that contains all sets under consideration i.e. it is a super set of each of the given sets. Such a set is called the universal set and is denoted by U. Thus a set that contains all sets in a…
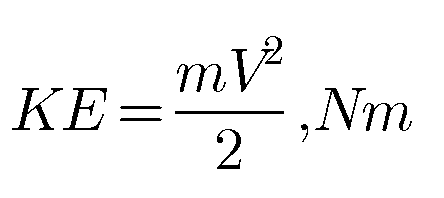
Energy in a state Stored energy is the energy possessed by a system. Stored energy in the system is called energy in a state. It is associated with a state. It change depends only on the end states of the process and not on the path of…
Difference of sets Let A and B be two sets. The difference of A and B written as A – B, is the set of all those elements of A which do not belong to set B Thus A – B={ x : x ∈ A and x ∉ B} or A – B={ x…
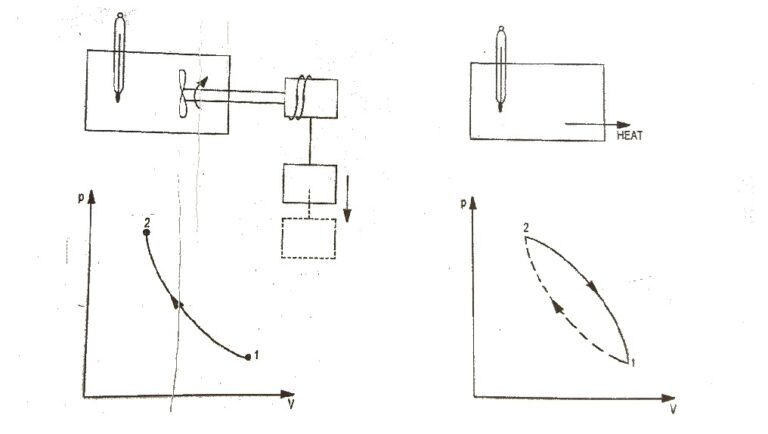
First Law of a Closed System Undergoing a Cycle : The first law of thermodynamics states that during any cycle a system undergoes the cyclic integral of heat is equal to the cyclic integral of the work. Fig.1 First Law of Thermodynamics To illustrates this, consider the gas as a system in…
Ordered pairs An ordered pairs consists of two objects or elements in a given fixed order. For example, if A and B are any two sets, then by an ordered pair of elements we mean a pair (a, b) in that order, where a ∈ A, b ∈…
Power set Let A be a set. Then the collection or family of all subsets of A is called the power set of A and is denoted by P(A). That is. P(A) = { S : S ⊂ A }. Since the empty set and the set A itself are subsets of A and are…