Venn Diagrams | Set
Venn diagrams
| Fig (ii) |
| Fig (iii) |
| Fig (i) |
| Fig (ii) |
| Fig (iii) |
| Fig (i) |
First Law for a Closed System Undergoing a Quasi-static process In many occasions it is necessary to consider a system undergoing a process rather than a cycle. The equation, ∮ dQ − ∮ dW = 0 is applicable during the system undergoing a cycle, and algebraic sum of all energies transfer across the system boundary…
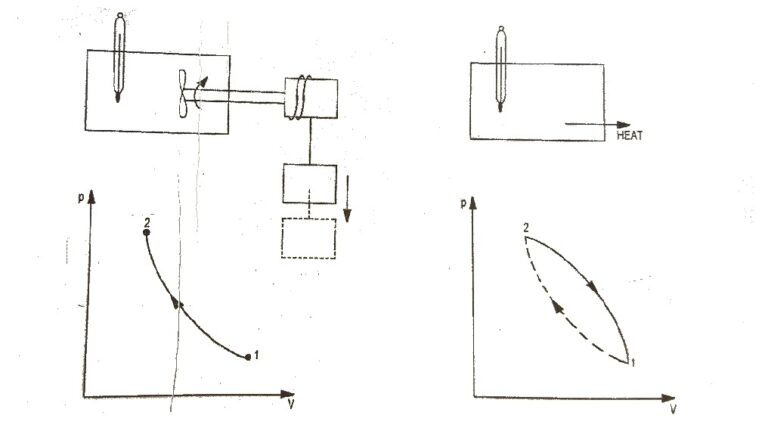
First Law of a Closed System Undergoing a Cycle : The first law of thermodynamics states that during any cycle a system undergoes the cyclic integral of heat is equal to the cyclic integral of the work. Fig.1 First Law of Thermodynamics To illustrates this, consider the gas as a system in…
Ideal gases The term gas is applied to a particular phase of a pure substance which will fills the system boundary, and no change of phase takes place or is contemplated. They always exist in gaseous form. For this reason, they have been called permanent gases. Perfect…
Function as a set of ordered pairs Let A and B be two non-empty sets. A relation f from A to B i.e a subset of A × B is called a function (or a mapping or a map) from A to B, if i) for each a ∈ A there exists b ∈ B…
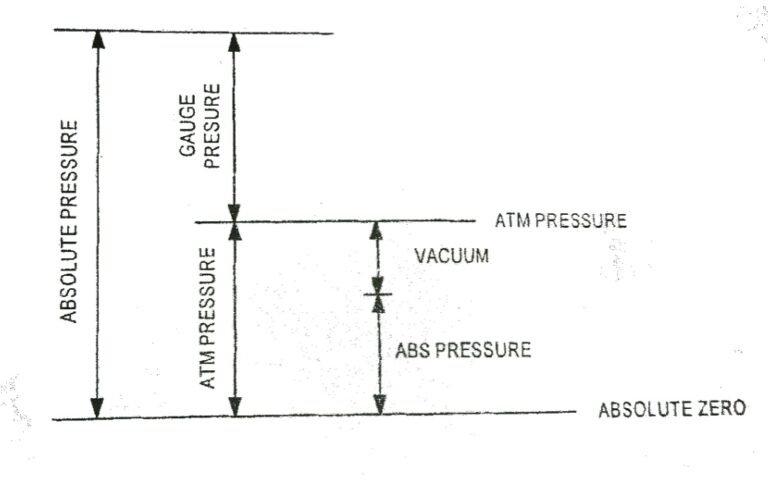
Pressure The molecules of a gas are in random motion. The rapidly moving molecules continually impact on the surface of the container and its effect is to produce a force over the surface. The force normal to unit area of surface is called pressure acting on the surface. The normal force exerted by the atmosphere…
Universal set In any discussion in set theory, there always happens to be a set that contains all sets under consideration i.e. it is a super set of each of the given sets. Such a set is called the universal set and is denoted by U. Thus a set that contains all sets in a…